How far is that star?

A clear, starry night is a wonderful sight.

That wonder may promote the question ‘how far away are those stars?

Stars are clearly a long way away.

Those distant suns appear as only tiny points of light.

Choose a single star, a lone point of light.

How far away is that star?

It seems almost impossible to measure the distance from your eyes to that point of light.

But by the end of this blog you will be able to answer that question.

You will be able to calculate the distance of stars for yourself.

Starfield around Orion.    Stellarium

The measurement is done  by using Earth’s orbit, precise observation and a bit of maths.

And something called parallax.

Parallax

Parallax is the apparent change of position of an object when seen from different viewpoints.

On a train journey, telegraph poles whizz by whilst a distant building seems to move very slowly.

The nearer the object, the greater the apparent change in position.

You can try a parallax experiment right now.

Just close one eye, hold up one finger and cover an object on the wall.

Open that eye and close the other.

Your finger seems to jump to the side.

But your finger didn’t move.

It was just seen from a different viewpoint.

Parallax animation by Nathaniel Domek

Nathaniel Domek’s animation shows how it works.

As we change viewpoint, objects in the distance seem to move more slowly than those that are nearby.

The white block moves more than distant green cube.

We can now use parallax to measure the distance of a star.

Star Parallax

We need a slightly bigger change of viewpoint than right eye / left eye.

So we’ll use the width of the Earth’s orbit.

That’s a pretty long baseline!

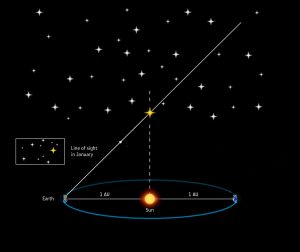
With our telescope we look at our chosen star, in January for example.

We plot its position against the starry background.

On our ESA diagram, our star is picked out in yellow.

It appears to the right of the photo box.

Star Parallax 1    Credit: ESA

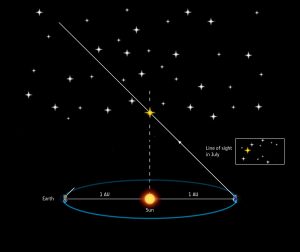
We then observe the star six months later, when we’re on the other side of the Earth’s orbit.

Star Parallax 2    Credit: ESA

We plot the position of our star again.

This time it appears to have moved, to the left of the photo box.

But the star didn’t move, we just changed our viewpoint.

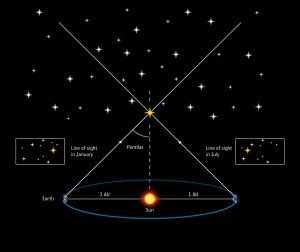
Something to note: the background stars are much further away, too far to show parallax.

They stay still, the same in both photos.

Now it’s time for the maths.

We can calculate how far away are the stars

Measuring the distance

Let’s first put our two observations together.

Star Parallax 3   Credit: ESA

Looking at the two photo boxes, we can see that our star has changed position.

We measure that change in an angle across the sky – the parallax angle.

And this is where our observation must be precise.

The parallax angle is tiny.

It is a fraction of a degree of arc.

Let’s put this in a context.

The Full Moon measures half a degree or 1800 seconds of arc.

The parallax angle of a star is less than one second of arc, a tiny distance.

But with our telescope we’ve been precise and we can measure it accurately.

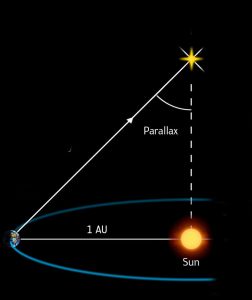
Let’s say our star has an apparent movement of 0.6 seconds.

For the maths, we halve this to fit the right-angled triangle in the diagram.

So the Parallax Angle becomes 0.3 seconds.

We have measured the Parallax Angle.

We know the distance of the Earth to the Sun – 150 million km.

With a bit of trigonometry, we can now calculate the height of our triangle.

This is the distance of the star.

Actually it’s quite easy.

It’s 1 divided by the parallax angle, a reciprocal, 1/ PA.

Let’s work out the distance of our star.

The Parallax Angle is 0.3 seconds.

So it’s distance is 1 / 0.3 = 3.33 

But 3.33 what?  What are the units of distance here?

And here’s the catch.

Our easy maths gives us a distance unit called the parsec – parallax second.

So our star is 3.33 parsecs away, 3.33pc.

The intuitive unit, more often used in the media, is light years.

One parsec is 3.26 light years.

To convert parsecs to light years we multiply by 3.26.

So our star is 3.33 x 3.26 LY = 10.8 light years away.

61 Cygni

The star I chose for our calculation is 61 Cygni.

It is circled on our star chart below.

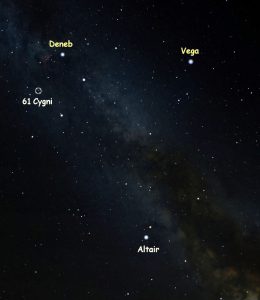
Summer Triangle & 61 Cygni.     Stellarium

This was actually the first star to have its distance measured.

The measurement was done in 1838 by German astronomer Wilhelm Bessell.

How far: limitations

Although parallax is a fairly accurate way of measuring star distances, it has significant limitations.

It only works with relatively close stars.

Parallax angles less than 0.01 arc seconds are difficult to measure using ground-based telescopes.

So the distance limit for parallax is around 100 parsecs or around 300 light years.

Beyond this, stars become part of the fixed starry background.

There are other indirect methods of estimating stellar distance.

But none are as accurate as the parallax technique.

Overcoming limitations: Hipparcos

Those limits apply to ground-based telescopes.

New space telescopes can measure the parallax of more distant stars.

The first mission was Hipparcos, the High Precision Parallax Collecting Satellite.

This nicely contrived acronym honours the ancient Greek astronomer Hipparchus of Nicaea.

Hipparcos measured parallax angles down to 0.001 seconds.

So it extended the range of star distances to 1000 parsecs, over 3000 light years.

Hipparcos satellite.   Credit: ESA

Hipparcos was active in the early 1990s.

By the end of its mission in 1993, it had measured the distances of over 118,000 stars.

Your turn!

Now it’s your turn to find the distance of some stars.

I’ve chosen three winter stars.

Two are from the constellation Orion, Betelgeuse and Rigel.

The other is our brightest night time star, Sirius.

Constellation of Orion with Sirius.    Stellarium

Sirius:  Credit: Akira Fujii 

So, imagine that you are an astronomer working with the Hipparcos project.

The satellite has  successfully measured the parallax of the three stars.

Now it is your job to calculate their distances.

Here are their observed parallax angles, p.

Betelgeuse = 0.006 seconds of ar

Rigel = 0.0029 seconds of arc

Sirius = 0.379 seconds of arc

You can now calculate the distance in parsecs, 1 / p.

Then you can convert the distance to light years by multiplying your answer by 3.26.

Distance = 1 / p = **parsecs x 3.26 = ** light years

Calculator ready?  Off you go!

You can check your answers at the end of this blog.

Overcoming limitations: Gaia

Hipparcos has been succeeded by Gaia, another space telescope.

Gaia was launched in 2013 and will last until 2025.

Gaia spacecraft.   Credit: ESA

Among many other star measurements, it will give distances of stars up to 100,000 light years.

And it will observe an incredible one billion stars.

You are an astronomer!

So did you calculate the distances of the three stars?

Can you answer the question ‘how far is that star’?

Here are the answers, using distance = 1 / parallax angle

Betelgeuse, distance = 1 / 0.006 = 166.6 parsecs = 543 light years

Rigel, distance = 1 / 0.0029 =  344.8 pc = 1,124 light years

Sirius, distance = 1 / 0.379 = 2.63 pc = 8.6 light years

If you got them all right, count yourself as an astronomer now!

And to add to your accolade, can you answer this question?:

Sirius is the brightest star as we see them from Earth.

But is it truly brighter than Betelgeuse and Rigel?

The author: Dennis Ashton is a Fellow of the Royal Astronomical Society and a Wonderdome presenter.

Would you like to hear more  Astronomy news?

Do you want to to find out about our upcoming public events?

Follow WonderDome Portable Planetarium on Twitter and Facebook or go to our web site wonderdome.co.uk